Second-order Møller–Plesset perturbation theory (MP2)#
Modules: pyscf.mp, pyscf.pbc.mp
The MP2 and coupled-cluster functionalities of PySCF are similar. See also Coupled-cluster theory.
Introduction#
Second-order Møller–Plesset perturbation theory (MP2) [26] is a post-Hartree–Fock method. MP2 calculations can be performed in PySCF with or without density fitting, depending on the initial SCF calculation.
Note also the existence of a native DF-MP2 implementation, which does not depend on the integral approximation in SCF, and which is significantly faster than the default implementation of MP2 with density fitting.
A simple example (see examples/mp/00-simple_mp2.py) of running an MP2 calculation is
#!/usr/bin/env python
#
# Author: Qiming Sun <osirpt.sun@gmail.com>
#
'''
A simple example to run MP2 calculation.
'''
import pyscf
mol = pyscf.M(
atom = 'H 0 0 0; F 0 0 1.1',
basis = 'ccpvdz')
mf = mol.RHF().run()
mf.MP2().run()
which outputs
converged SCF energy = -99.9873974403487
E(MP2) = -100.198764900659 E_corr = -0.211367460310054
namely, the Hartree–Fock energy, the MP2 energy and their difference, the MP2 correlation energy.
Note
The last line in the code example above could have been replaced by
pyscf.mp.MP2(mf).kernel()
or
pyscf.mp.MP2(mf).run()
for the same result.
Spin symmetry#
The MP2 module in PySCF supports a number of reference wavefunctions with broken spin symmetry. In particular, MP2 can be performed with a spin-restricted, spin-unrestricted, and general (spin-mixed) Hartree-Fock solution, leading to the RMP2, UMP2, and GMP2 methods.
The module-level mp.MP2(mf) constructor can infer the correct method based
on the level of symmetry-breaking in the mean-field argument. For more explicit
control or inspection, the respective classes and functions can be found in
mp2.py (restricted), ump2.py (unrestricted), and gmp2.py
(general).
For example, a spin-unrestricted calculation on triplet oxygen can be performed as follows:
from pyscf import gto, scf, mp
mol = gto.M(
atom = 'O 0 0 0; O 0 0 1.2', # in Angstrom
basis = 'ccpvdz',
spin = 2
)
mf = scf.HF(mol).run() # this is UHF
mymp = mp.MP2(mf).run() # this is UMP2
print('UMP2 total energy = ', mymp.e_tot)
Properties#
A number of properties are available at the MP2 level.
Unrelaxed 1- and 2-electron reduced density matrices can be calculated. They are returned in the MO basis:
dm1 = mymp.make_rdm1()
dm2 = mymp.make_rdm2()
Analytical nuclear gradients can be calculated [27, 28, 29]
mygrad = mymp.nuc_grad_method().run()
Frozen orbitals#
By default, MP2 calculations in PySCF correlate all electrons in all available
orbitals. To freeze the lowest-energy core orbitals, use
the frozen keyword argument:
mymp = mp.MP2(mf, frozen=2).run()
To freeze occupied and/or unoccupied orbitals with finer control, a
list of 0-based orbital indices can be provided as the frozen
keyword argument:
# freeze 2 core orbitals
mymp = mp.MP2(mf, frozen=[0,1]).run()
# freeze 2 core orbitals and 3 unoccupied orbitals
mymp = mp.MP2(mf, frozen=[0,1,16,17,18]).run()
The number of core orbitals to be frozen can be generated automatically:
mymp = mp.MP2(mf).set_frozen().run()
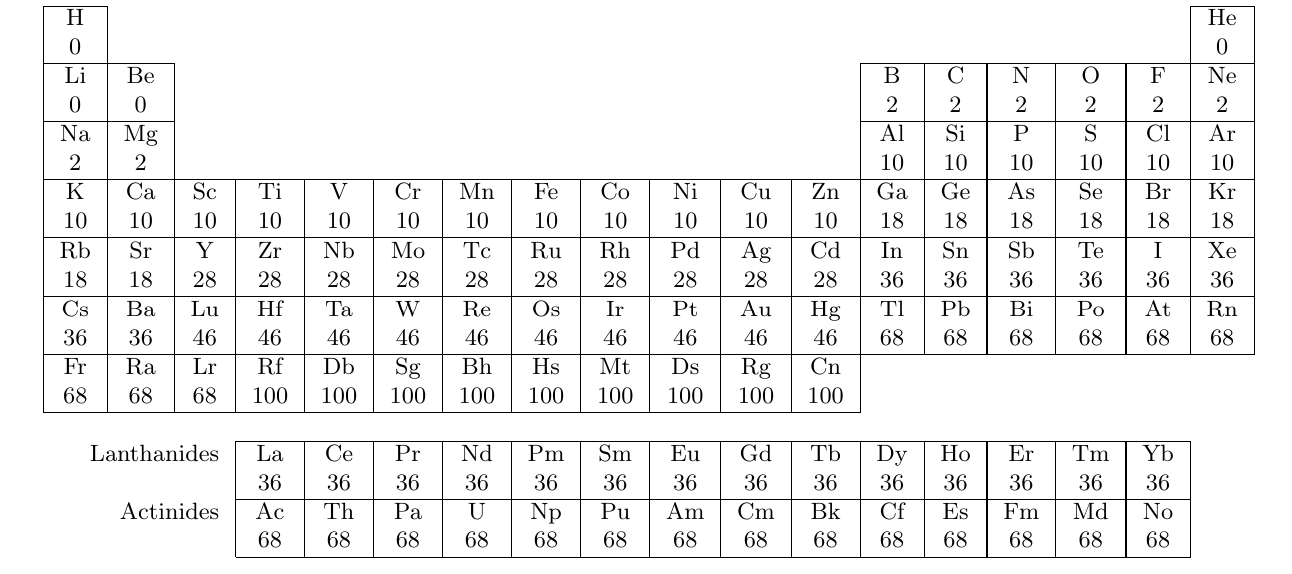
set_frozen() will freeze the core orbitals determined by sum of the core electrons of atoms, which are shown as follows.
The current rule is the same as that of ORCA program.
Job control#
Avoid t2 storage#
If the t2 amplitudes are not required after the MP2 calculation, they don’t need to be saved in memory:
mymp = mp.MP2(mf)
# by default, with_t2=True
mymp.kernel(with_t2=False)
Density-fitted MP2 (DF-MP2)#
Background#
MP2 can be combined to great benefit with density fitting (DF), also known as the resolution of the identity (RI) approximation. While the formal scaling remains \(O(N^5)\), the prefactor and the overall computational cost are reduced strongly, so that calculations can be performed on much larger molecules than with conventional MP2. Provided that a suitable auxiliary basis set is used, the resulting DF/RI errors in reaction energies, geometries, properties etc. are negligible compared to the intrinsic errors of MP2.
This implementation can calculate energies, as well as unrelaxed and relaxed one-particle density matrices. Analytical gradients are not available yet. RHF and UHF references are supported throughout.
Please note that this part of the documentation does not describe the older mp.dfmp2.DFMP2
implementation, which is still returned by the density_fit() method of the mp.mp2.MP2
class; instead it is about the newer DFRMP2 and DFUMP2 classes, which need to be imported
directly from mp.dfmp2_native or mp.dfump2_native at present.
Using the DF-MP2 implementation#
For technical reasons (incompatible algorithms), the “native” DF-MP2 implementation is not
implemented as a subclass of mp.mp2.MP2, but it is written as an independent class instead.
Currently, the classes DFRMP2 (for RHF references) and DFUMP2 (for UHF references) need to
be imported from the respective modules mp.dfmp2_native and mp.dfump2_native:
from pyscf.mp.dfmp2_native import DFRMP2
from pyscf.mp.dfump2_native import DFUMP2
Both modules also make the respective classes available under the alias DFMP2. The file
examples/mp/10-dfmp2.py contains a simple example for a DF-MP2 energy calculation.
There is also an older variant of DF-MP2 implemented in mp.dfmp2, which does not exploit the
advantages of density fitting fully, and may therefore have much higher memory demands for larger
molecules. Please note that the density_fit() method of the conventional mp.mp2.MP2 class
provides an instance of the old implementation, not the new one! Currently, the “native”
implementation can only be used by importing it from mp.dfmp2_native or mp.dfump2_native
directly as shown above.
Unless specified by the user, an appropriate auxiliary basis set is determined automatically. Note
that there exist different auxiliary basis sets for Coulomb and exchange fitting in DF-HF on the one
hand, and for correlation fitting in MP2 or other dynamic correlation methods on the other hand.
The DF approximation in MP2 does not depend on the approximation taken for SCF. Arbitrary
auxiliary sets can be specified with the auxbasis option:
DFMP2(mf, auxbasis='cc-pVTZ-RI')
In RHF-DF-MP2 calculations, orbitals can be frozen by specifying either an integer, or a list. Frozen core UHF-DF-MP2 calculations are initiated by providing either an integer, or two lists of equal length (for the alpha and beta orbitals):
DFRMP2(mf, frozen=2)
DFRMP2(mf, frozen=[0, 1])
DFUMP2(mf, frozen=2)
DFUMP2(mf, frozen=([0, 1], [0, 2]))
DF-MP2 densities#
Relaxed and unrelaxed 1-RDMs can be calculated for the RHF and UHF variants of the “native” DF-MP2 implementation. The points below provide some advice on choosing the correct type of MP2 density.
The relaxed density should be used to calculate properties if the MP2 method is well-behaved for the system in question. Properties calculated thereby correspond to the correct derivative of the MP2 energy with respect to an appropriate external perturbation. This is illustrated in examples/mp/11-dfmp2-density.py, where the dipole moment of chloromethane is calculated much more accurately with the relaxed density than with the unrelaxed one. To calculate the relaxed density, a set of CP-SCF type equations needs to be solved in one of the steps. In ill-behaved systems, for example if there is multi-reference character, the MP2 natural occupation numbers can be substantially larger than two or smaller than zero.
A typical use case for the unrelaxed density is to calculate starting orbitals for a CASSCF calculation, which can be used despite the system being described poorly at MP2 level otherwise. In contrast to the relaxed density, the natural occupation numbers of the unrelaxed density are always between two and zero. examples/mp/12-dfump2-natorbs.py shows how to calculate natural orbitals for the allyl radical, which has a significantly spin-contaminated UHF wave function. On the other hand, the unrelaxed density will often give very poor results for properties (such as electrostatic moments).
Spin-component scaling#
Spin-component scaled (SCS-)MP2 calculations can be performed analogously to DF-MP2 calculations
using the classes SCSDFRMP2 and SCSDFUMP2, which also have got aliases such as SCSMP2
inside the respective modules. The default scaling factors can be changed to arbitrary values:
from pyscf.mp.dfmp2_native import SCSMP2
pt = SCSMP2(mf, ps=6/5, pt=1/3)
pt.kernel()
